Aristarchus of Samos (310 BC - 230 BC) was the first to estimate the apparent diameter of the Moon in relation to that of the Earth.
Having observed during an eclipse of the Moon, that it remained for almost two hours in the shadow of the Earth, and having observed that the Moon moved by its own diameter in an hour of time, he was able to conclude that the lunar diameter is about three times smaller than the terrestrial diameter.
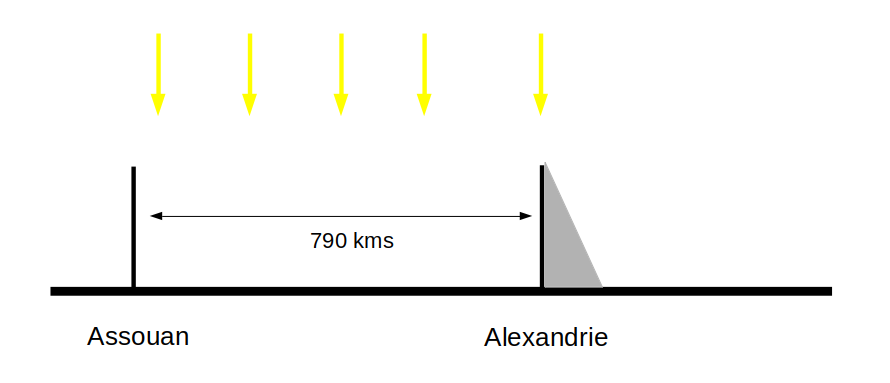
Around the same time, another Greek astronomer, Eratosthene de Cyrene (276 BC - 198 BC) calculated with a good approximation the diameter of the Earth. Indeed, having planted two sticks in Egypt, one in Aswan, the other in Alexandria, he noted that at noon on the same day, the stick of Aswan did not cast any shadow, but that of Alexandria had a shadow of 7.2 °. The distance between these two cities being 790 kms, we can therefore calculate the circumference of the Earth as follows:
$$ circumference = {790*360 \over 7.2} = 39 500 kms$$The diameter of the earth can therefore also be calculated from the equation:
$$ diameter = {39,500 \over π} = 12,573 kms$$
Note that the diameter of the Earth is 12,758 km. Also, the ratio between the diameter of the Earth and that of the Moon is approximately: 3.7

Now hat you know the diameter of the Moon (3,474 km), and since the apparent size of the full moon in the sky is approximately 0.51 degrees, could you guess the distance between the Moon and Earth? (tip: you can check the equation in this article)
Post a comment
| Date | Name | Comment |
|---|