Show me the sky!

Imagine holding an apple at arm's length and looking at it. The apple appears to cover a certain portion of your field of view. Now, imagine the entire sky as your field of view, from one horizon to the other. The apparent size of the apple in degrees is like measuring how much of that entire sky it would cover if you could place it far away. So, if the apple appears to cover a small area of the sky, it has a small apparent size in degrees (symbol: °). On the other hand, if the apple appears to cover a larger area of the sky, it has a larger apparent size in degrees. The apparent size in degrees helps us understand how much space an object appears to occupy in our view of the sky.

The equation below allows us to calculate the apparent size (δ) for an object of size (d) located at a distance (D):

$$ δ = {arctan({d \over 2*D})*{360 \over π}}$$

For example, considering that the Moon is, on average, 384,400 km away from Earth, and its diameter is 3,474 km, its average apparent diameter is approximately 0.51°.

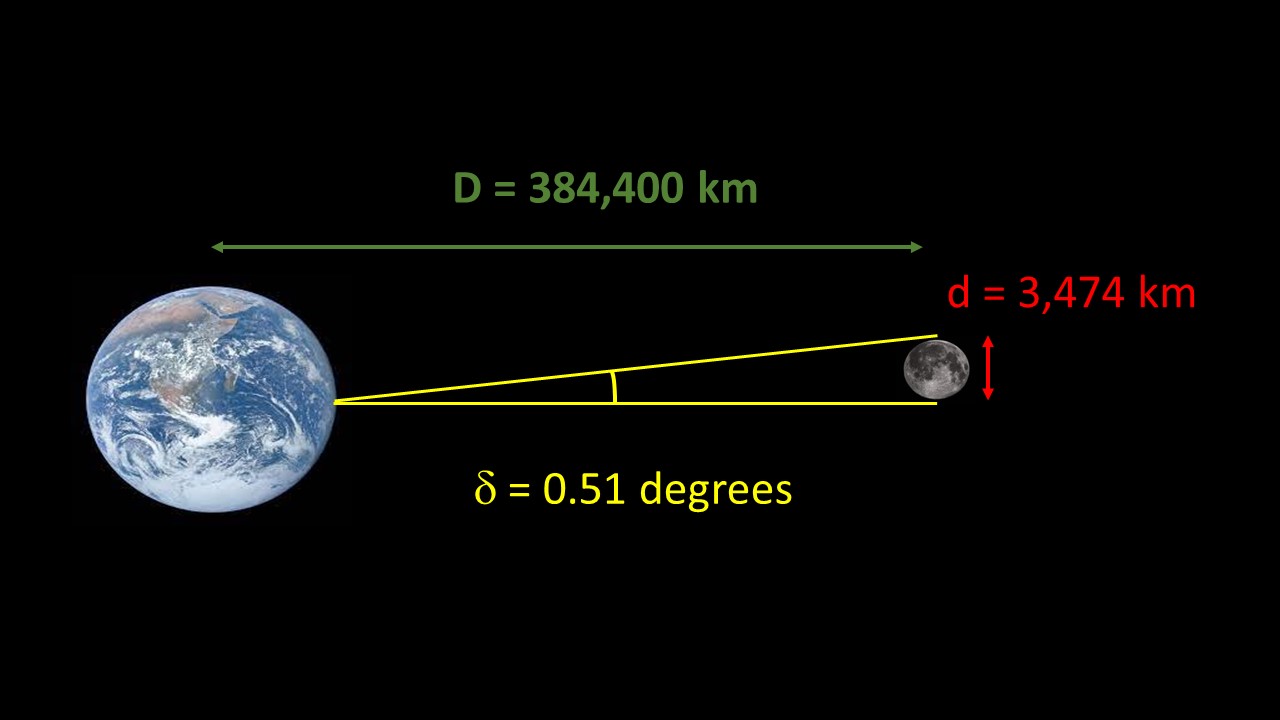
Note that in astronomy, apparent sizes are often represented by small values. For practical reasons, these values are expressed in either arcminutes (symbol: ') or arcseconds (symbol: "). To convert the results to arcminutes (or arcseconds), simply multiply the values obtained in degrees by 60 (or 3,600). Thus, the apparent size of the Moon is 31 arcminutes (31') or 1,860 arcseconds (1,860").

It's important to note that since the planets in our solar system orbit the Sun, the distance between us and each planet varies from day to day, affecting the apparent diameter of objects in the solar system.

If you wish to determine the apparent size at a specific observation time, you can consult the ephemeris of the main objects in the solar system.

Select an object MercuryVenusMarsJupiterSaturnUranusNeptunePlutoVestaCeresMoonSun